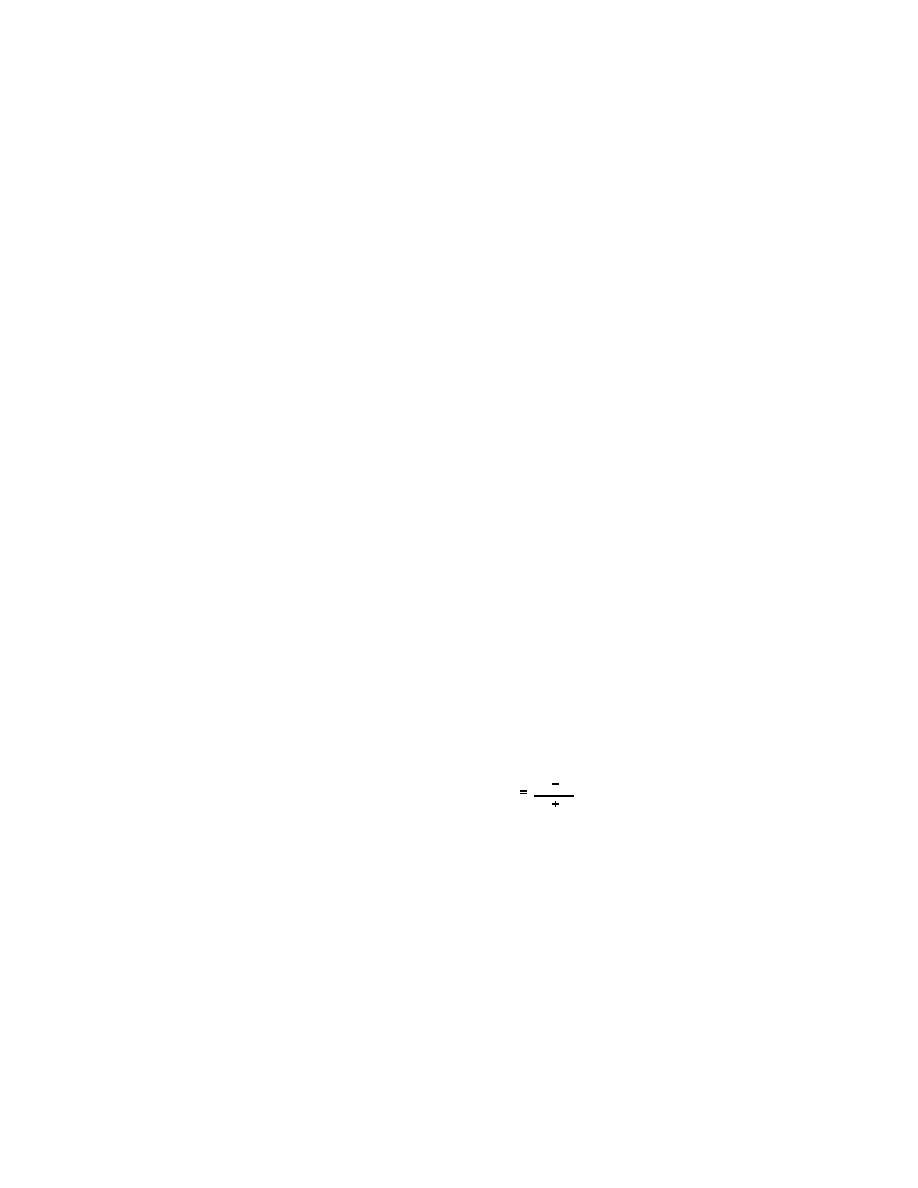
EP 1110-2-12
30 Sep 95
first performed on the dam-foundation model without
Appendix D shows the pressure function curves for
added mass (which represents the empty reservoir
reservoir bottom conditions with wave reflection
condition), and then a second dynamic analysis was
coefficients of 0.50 and 0.75. As apparent from these
performed on the model with added mass. The
curves, the hydrodynamic pressure increases with an
difference in the unbalanced nodal forces between
increase in the reflection coefficient.
these two analyses represented the hydrodynamic
forces exerted on the nodes. From these nodal forces
b. Effects of Rw. When the fundamental vibra-
the pressure distribution was readily determined.
tion period of impounded water and the fundamental
period of the dam are approximately equal, Rw
f. Comparison of hydrodynamic methods.
approaches 1.0. This condition indicates the approach
Although Chopra's Simplified Procedure is only an
of a state of resonance, and the pressure function then
approximate procedure based on the standard funda-
becomes quite large for a nonabsorptive reservoir
mental mode shape and simplified methods for deter-
bottom. In contrast, the pressure function for an
mining the required periods of vibration, it is
absorptive bottom is much less affected by the
assumed that the procedure provides hydrodynamic
approach of resonance, because the effect of reservoir
loading that is at least within the general order of
bottom absorption is to reduce the large resonant
accuracy expected in dynamic analyses. On this
displacement peaks.
basis, the equivalent mass system based on Wester-
gaard's formula (Plot 2), underestimated the hydrody-
c. Estimating reservoir bottom absorption.
namic loading on the typical dam section by about
Assuming a nonabsorptive reservoir bottom may lead
40 percent. The equivalent mass system developed
to an overly conservative hydrodynamic response for
by the method described in Appendix D produced
dams when the earthquake load condition includes a
hydrodynamic loading (Plot 3) which correlated
high forebay pool. The degree of adsorptiveness
reasonably well with Chopra's Simplified Procedure.
characterized by the wave reflection coefficient is
On this basis, the method described in Appendix D,
usually difficult to determine reliably. The value of
which uses the standard pressure function curves, is
the wave reflection coefficient will likely increase
recommended for developing the equivalent mass
during the life of the dam as sediments are continu-
system.
ously deposited. Therefore, it is recommended that
the effects of reservoir bottom absorption be included
g. Hydrodynamic contribution to response. For
in the dynamic analysis by using a wave reflection
high pool conditions, a large portion of the dynamic
coefficient based on the properties of the impounded
response is attributable to the hydrodynamic effect.
water and the foundation rock, and neglect the addi-
In the example that produced Plot 3 in Figure 7-3,
tional adsorptiveness due to sediments that will even-
47 percent of the total equivalent mass system con-
tually be deposited (Fenves and Chopra 1984). The
sisted of the added mass representing the hydrody-
wave reflection coefficient is determined by the fol-
namic effects. Therefore, the equivalent mass system
lowing equation:
will significantly affect the response for pool depths
greater than about half of the height of the dam.
k
1
α
k
1
7-6.
Reservoir Bottom Absorption
where
a. Wave reflection coefficient. The nonrigid
reservoir bottom partially absorbs incident hydrody-
α = wave reflection coefficient
namic pressure waves. This moderates the increase
k = ρC/ρrCr
in response of the dam due to the dam's interaction
with the impounded water. This is readily apparent
ρ = mass density of water = 1.938 (lb-sec2) /ft4
by comparing the standard hydrodynamic pressure
function curves for two different reservoir bottom
C = velocity of pressure waves in water =
absorption conditions. Reservoir bottom absorption is
4,720 ft/sec
expressed by a wave reflection coefficient which
ρr = mass density of the foundation rock in
varies from zero for a fully absorptive condition to
(lb-sec2) /ft4
1.0 for a fully reflective condition. Figure D-4 in
7-7



 Previous Page
Previous Page
